Wzory doboru próby

Dobór próby może zostać wykonany według wielu metod (opisywanych w artykule „Metody doboru próby audytowej”). Mimo, że próba może zostać (i zazwyczaj jest) dobierana bez przeprowadzania kalkulacji (w odróżnieniu od definiowania wielkości próby), kalkulacja kilku elementów może być pomocna. Jednocześnie przydatna może okazać się przedstawiona w dalszej części artykułu tablica, która może zastąpić generator liczb losowych.

Systematyczny dobór próby

Systematyczny dobór próby polega na wybieraniu co któregoś elementu, np. co dziesiąty element z populacji. Mając informację o wielkości populacji oraz o wielkości próby (skalkulowanej według wzorów doboru wielkości próby) można zastosować poniższy wzór doboru próby.

• Wyznaczanie pozycji startowej i pierwszego elementu próby
  
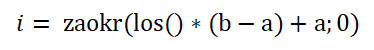
  Legenda:
  a – pierwszy element populacji / pierwszy numer id elementu populacji
  b – ostatni element populacji / ostatni numer id elementu populacji
  i – pozycja startowa

• Wyznaczanie „odległości” pomiędzy elementami próby
  
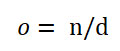
  Legenda:
  n – wielkość populacji
  d – wielkość próby
  o – „odległość” pomiędzy elementami próby

• Wyznaczanie pozostałych elementów próby
  
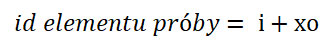
  Legenda:
  x – liczba naturalna przybierająca wartości od 1 do d
  d – wielkość próby
  o – „odległość” pomiędzy elementami próby
  i – pozycja startowa           

Zalety

Zaletą wyboru systematycznego jest łatwość stosowania tej metody doboru próby.

Wady

W przypadku nielosowego ułożenia populacji metoda doboru systematycznego także nie jest losowa. Jest to najbardziej widoczne w przypadku, gdy pewien trend w populacji (także w jej ułożeniu) jest tak częsty, jak „odległość” pomiędzy elementami próby.

Kiedy stosować

Metodę można stosować zawsze, gdy mamy pewność, że ułożenie populacji nie ma trendu, który mógłby spowodować, że wybrana próba nie jest losowa.

Tablice liczb losowych wygenerowanych przez Excel

Poniższe tablice prezentują liczby wygenerowane w Excelu funkcją zaokr(los()*(b-a)+a;0) w różnych, rozłącznych przedziałach. Dzięki odpowiedniemu wykorzystaniu pierwszej kolumny z przedziału od 1 do 8 można losować, z której kolumny populacji (jako że jest ich dokładnie 8) powinny być losowane pozycje do próby. Dla przykładu pod tabelą zaprezentowany został proces losowania.

Przykład losowania 3 pozycji dla populacji mającej 8 tys. elementów:

• Wybieramy 3 elementy z kolumny z zakresem od 1 do 8. Z uwagi na ich losowe ułożenie mogą być to elementy wybierane po kolei, czyli 6, 7 i 7 (można jednak je losować).
• Pobieramy pierwszą pozycje z kolumny 6, czyli 5.921. Pobieramy pierwszą pozycję z kolumny 7, czyli 6.045 oraz drugi element z kolumny 7, czyli 6.456.
• Z populacji do próby wylosowano pozycje pod numerami indeksacyjnymi: 5.921, 6.045 oraz 6.456.

Zalety

Metoda doboru próby z zastosowaniem tablic liczb losowych jest bardzo prostą metodą do stosowania, gdyż z tablicy wyczytujemy dokładne elementy populacji, które są wybierane do próby.

Wady

Wielkość populacji powinna być zgodna z tym, jak są ułożone tabele liczb losowych. Biorąc za przykład powyższą tablicę liczb losowych, można ją zastosować dla populacji o 8 tys. elementów lub 1 tys. elementów (wtedy rezygnujemy z losowania lub wybierania kolumn, gdyż bierzemy po kolei pozycje z kolumny pierwszej mającej losowe liczby od 1 do 1000). Inną wadą jest to, że dla bardzo dużych prób tablice muszą być większe.

Kiedy stosować

Metodę można stosować dla wybranych populacji (gdy są one zsynchronizowane z tablicami), dla niewielkich prób.